Колінеарна система і приклади
The колінеарні вектори Вони є одним з трьох типів існуючих векторів. Мова йде про ті вектори, які знаходяться в одному напрямку або лінії дії. Це означає наступне: два або більше векторів будуть колінеарними, якщо вони розташовані прямолінійно, паралельно один одному.
Вектор визначається як величина, що застосовується до тіла і характеризується як має напрямок, сенс і шкалу. Вектори можна знайти в площині або в просторі і можуть бути різних типів: колінеарні вектори, паралельні вектори і паралельні вектори.

Індекс
- 1 колінеальні вектори
- 2 Характеристики
- 2.1 Приклад 1
- 2.2 Приклад 2
- 2.3 Приклад 1
- 3 Колінеарна векторна система
- 3.1 Колінеарні вектори з протилежними сенсами
- 3.2 Колінеарні вектори з однаковим сенсом
- 3.3 Колінеарні вектори з однаковими величинами і протилежними почуттями
- 4 Різниця між колінеарними і паралельними векторами
- 5 Посилання
Колінеарні вектори
Вектори колінеарні, якщо лінія дії одного є точно такою ж лінією дії всіх інших векторів, незалежно від розміру і сенсу кожного з векторів..
Вектори використовуються як уявлення в різних областях, таких як математика, фізика, алгебра, а також у геометрії, де вектори колінеарні тільки тоді, коли їх напрямок є однаковим, незалежно від того, чи їх значення не є.
Особливості
- Два або більше векторів є колінеарними, якщо залежність між координатами однакова.
Приклад 1
Маємо вектори m = m_x; m_y і n = n_x; n_y. Вони колінеарні, якщо:
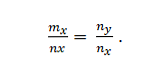
Приклад 2
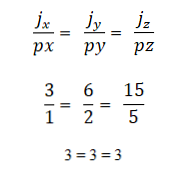
- Два або більше векторів колінеарні, якщо множення продукту або вектора дорівнює нулю (0). Це відбувається тому, що в системі координат кожен вектор характеризується відповідними координатами, і якщо вони пропорційні один одному, вектори будуть колінеарними. Це виражається таким чином:
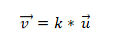
Приклад 1
Маємо вектори a = (10, 5) і b = (6, 3). Щоб визначити, чи є вони колінеарними, застосовується детермінантна теорія, яка встановлює рівність перехресних продуктів. Таким чином, ви повинні:
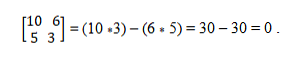
Колінеарна векторна система
Колінеарні вектори представлені графічно, використовуючи напрямок і сенс цих - враховуючи, що вони повинні проходити через точку застосування - і модуль, який є певною шкалою або довжиною..
Система колінеарних векторів формується, коли два або більше векторів діють на об'єкт або тіло, що представляє силу і діє в одному і тому ж напрямку.
Наприклад, якщо на тіло застосовані дві колінеарні сили, то їх буде залежати тільки від того, в якому напрямку вони діють. Є три випадки:
Колінеарні вектори з протилежними відчуттями
Отримана з двох колінеарних векторів дорівнює сумі цих:
R = Σ F = F1 + F2.
Приклад
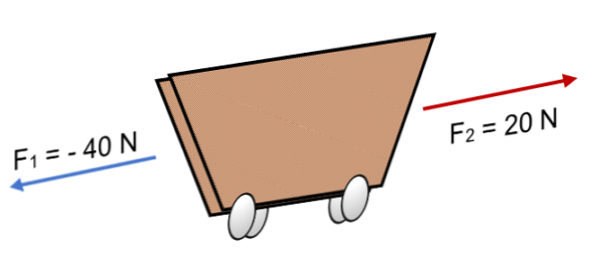
Якщо на візок F діють дві сили1 = 40 N і F2 = 20 N у зворотному напрямку (як показано на зображенні), результат:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
Колінеарні вектори з однаковим сенсом
Величина результуючої сили буде дорівнює сумі колінеарних векторів:
R = Σ F = F1 + F2.
Приклад
Якщо на візок F діють дві сили1 = 35 N і F2 = 55 N в тому ж напрямку (як показано на зображенні), результат:
R = Σ F = 35 N + 55N.
R = 90 N.
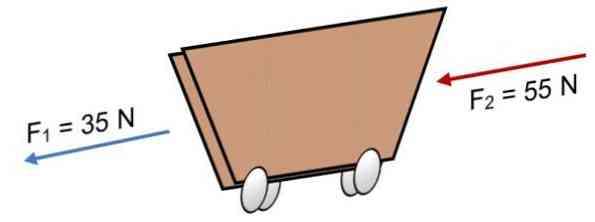
Позитивний результат вказує на те, що колінеарні вектори діють вліво.
Колінеарні вектори з однаковими величинами і протилежними сенсами
Отримана з двох колінеарних векторів буде дорівнює сумі колінеарних векторів:
R = Σ F = F1 + F2.
Оскільки сили мають однакову величину, але в протилежному напрямку, тобто один буде позитивним, а інший негативним, при додаванні двох сил результуюча буде дорівнює нулю.
Приклад
Якщо на візок F діють дві сили1 = -7 N і F2 = 7 N, які мають однакову величину, але у зворотному напрямку (як показано на зображенні), результатом є:
R = Σ F = (-7 N) + 7N.
R = 0.
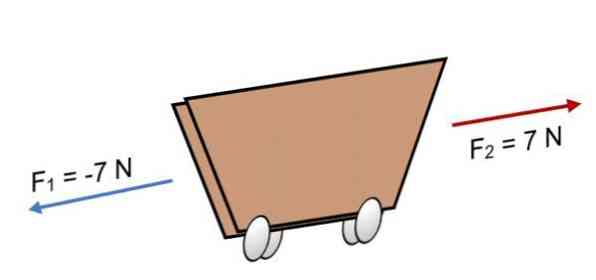
Оскільки результуюча величина дорівнює 0, це означає, що вектори врівноважені один з одним і, отже, тіло знаходиться в рівновазі або в стані спокою (воно не рухається).
Різниця між колінеарними і паралельними векторами
Колінеарні вектори характеризуються тим, що мають однаковий напрямок на одній лінії, або тому, що вони паралельні лінії; тобто вектори прямих паралельних ліній.
З іншого боку, одночасні вектори визначаються, оскільки вони знаходяться в різних лініях дії, які перехоплюються в одній точці.
Іншими словами, вони мають однакову точку виникнення або прибуття - незалежно від їхнього модуля, напряму чи напрямку, - утворюючи кут між ними.
Системи паралельних векторів вирішуються математичними методами або графіками, які є методом паралелограма сил і методу багатокутника сил. Через це буде визначено значення результуючого вектора, який вказує напрямок руху тіла.
В основному, основною відмінністю між колінеарними векторами і паралельними векторами є лінія дії, в якій вони діють: колінеарні ті діють в одній лінії, тоді як паралельні в різних.
Тобто колінеарні вектори діють в одній площині, "X" або "Y"; і одночасно діють в обох площинах, починаючи з тієї ж точки.
Колінеарні вектори не знаходяться в точці, так само як і паралельні, тому що вони паралельні один одному.
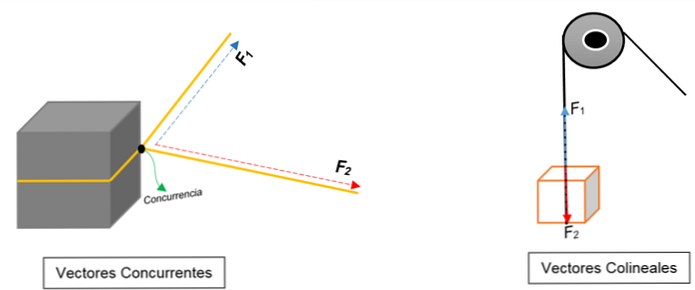
У лівому зображенні можна побачити блок. Вона пов'язана мотузкою, а вузол розділяє її на два; коли тягнуться до різних орієнтацій і з різними силами, блок рухатиметься в тому ж напрямку.
Представлені два вектори, які збігаються в точці (блоці), незалежно від їх модуля, сенсу або напрямку.
Натомість у правому зображенні з'являється шківа, що піднімає коробку. Канат являє собою лінію дії; коли вона витягується, на неї діють дві сили (вектори): одна сила натягу (при підйомі на блок) і інша сила, яка надає вагу блоку. Обидва мають однаковий напрямок, але в протилежних напрямках; не збігаються в одній точці.
Список літератури
- Estalella, J. J. (1988). Векторний аналіз. Том 1.
- Gupta, A. (s.f.). Освіта Tata McGraw-Hill.
- Jin Ho Kwak, S.H. (2015). Лінійна алгебра. Springer Science & Business Media.
- Montiel, H. P. (2000). Фізика 1 для технологічного бакалавра. Редакційна група Patria.
- Сантьяго Бурбано де Ерчилла, C. G. (2003). Загальна фізика Редакційний Тебар.
- Sinha, K. (s.f.). Текстова книга з математики XII т. 2. Растогі видання.


