Скільки країв має гексагональна призма?

Знати скільки ребер має гексагональна призма значення "край", "призма" і "гексагональна" повинні бути відомі. Перші два поняття є загальними визначеннями, а третя концепція пов'язана з формою геометричної фігури.

Говорячи про шестикутні, згадується шестикутник (багатокутник). Префікс "hexa" вказує, що багатокутник має шість сторін.

Край є краєм об'єкта. Геометрично це лінія, яка з'єднує дві послідовні вершини геометричної фігури.

Призма - це геометрична фігура, обмежена двома базами, які є паралельними і рівними багатокутниками, а їх бічні грані - паралелограми.

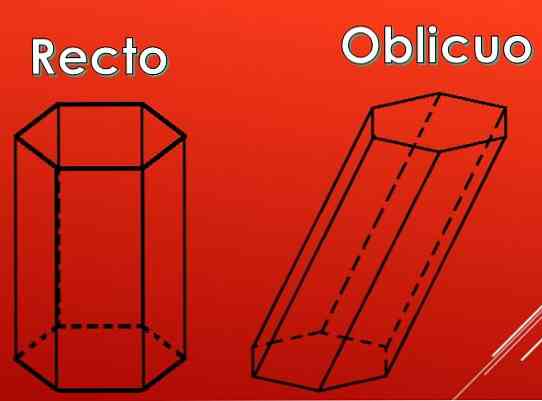
На наступному зображенні видно, що бічні грані гексагональної призми можуть бути прямокутниками, але вони також можуть бути паралелограмами.

За типом паралелограм, премії можна розділити на два типи: прямий і косий.

Як порахувати краї гексагональної призми?

Кількість ребер, які має гексагональна призма, не змінюється, якщо вона є прямою або косою призмою. Також число ребер також не залежить від довжини сторін.

Підрахунок крайок гексагональної призми можна здійснити кількома способами. Ось два способи:

1- Розкладайте призму

Один із способів підрахувати ребра - це розкладання гексагональної призми у двох її підставах та її бічних гранях. Таким чином ви отримуєте два шестикутники і паралелограм з п'ятьма внутрішніми лініями.

Кожен шестикутник має шість ребер, тому призма буде мати більше 12 ребер.

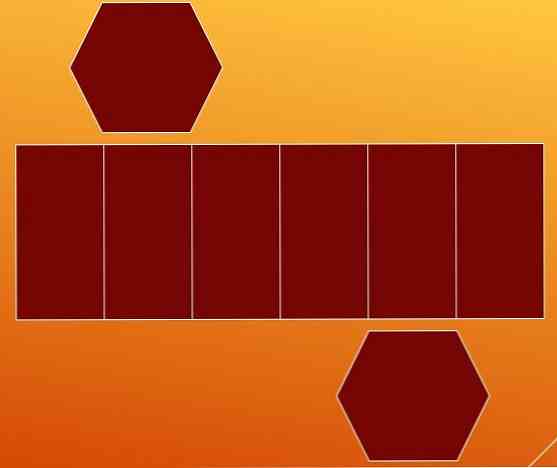
На перший погляд вважається, що паралелограма містить дев'ять ребер (сім вертикальних і два горизонтальних). Але зручно зупинитися, щоб проаналізувати цей випадок.

Коли паралелограм зігнути до форми призми, видно, що перша лінія зліва буде з'єднуватися з останньою лінією праворуч, з якою обидві лінії являють собою єдине ребро.

А як щодо двох горизонтальних ліній?

Коли всі шматки знову зібрані, горизонтальні лінії будуть з'єднані, кожна з них, з шістьма краями кожного шестикутника. З цієї причини підрахунок їх окремо буде помилкою.

Таким чином, паралелограма містить шість ребер призми, які разом з 12 ребрами, що нараховуються на початку, дають всього 18 ребер.

2.- Проектування кожного краю

Інший спосіб, багато простіший для підрахунку ребер, полягає в тому, що основи гексагональних призм є шестикутними, тоді кожна база має шість ребер.

З іншого боку, з кожної вершини шестикутника єдине ребро проектується на відповідну вершину іншого шестикутника; тобто є шість ребер, які з'єднують одну базу з іншою.

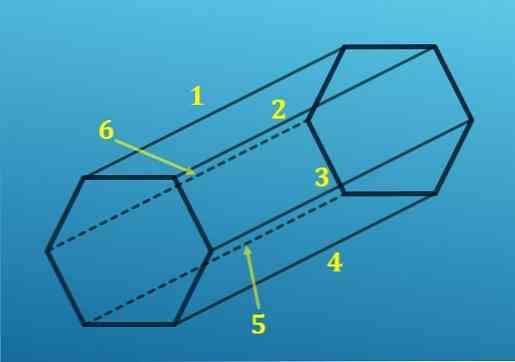
Додавши всі ребра, ви отримаєте всього 18 ребер.

Висновок

Можна показати, що число ребер призми дорівнює трьохкратному числу ребер, які утворює його багатокутник..

Отже, п'ятикутна призма матиме 3 * 5 = 15 ребер, семикутне призма буде мати 3 * 7 = 21 ребер і таким чином може бути застосована до будь-якої призми.

Список літератури

1. Білштейн, Р., Лібескінд, С., і Лотт, Дж. В. (2013). Математика: підхід до вирішення проблем для вчителів базової освіти. Лопес Матеос.
2. Fregoso, R. S., & Carrera, S.A. (2005). Математика 3. Редакція Progreso.
3. Gallardo, G., & Pilar, P. M. (2005). Математика 6. Редакція Progreso.
4. Gutiérrez, C.T., & Cisneros, M. P. (2005). Третій курс з математики. Редакція Progreso.
5. Kinsey, L., & Moore, T.E. (2006). Симетрія, форма і простір: вступ до математики через геометрію (проілюстровано, передрукована редакція). Springer Science & Business Media.
6. Mitchell, C. (1999). Сліпуче дизайну лінії Math (Ілюстрований ред.). Scholastic Inc.
7. Р., М. П. (2005). Я малюю 6º. Редакція Progreso.