Особливості семикутної призми і як обчислити обсяг

A семикутної призми є геометричною фігурою, яка, як випливає з назви, включає дві геометричні визначення: призму і семикутник.

"Призма" являє собою геометричну фігуру, обмежену двома базами, рівними і паралельними багатокутниками, а їх бічні грані паралелограм.

"Шестикутник" являє собою багатокутник, який утворений семи (7) сторонами. Оскільки семикутник є багатокутником, він може бути регулярним або нерегулярним.

Полігон називається регулярним, якщо всі його сторони мають однакову довжину, а їхні внутрішні кути - однакові, їх ще називають рівносторонніми багатокутниками; інакше кажуть, що багатокутник нерегулярний.

Характеристика семикутної призми

Нижче наводяться деякі особливості, що мають семикутну призму, таку як: її конструкція, властивості її основ, площа всіх її граней і її обсяг.

1- Будівництво

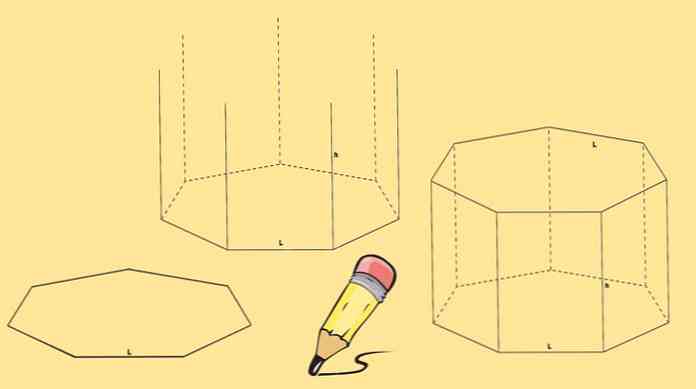
Для побудови семикутної призми потрібні дві гексагони, які будуть її основи і сім паралелограм, по одній на кожній стороні семикутника.

Почніть з малювання семикутника, потім намалюйте сім вертикальних ліній рівної довжини, які надходять від кожної його вершини.

Нарешті черговий семиугольник малюється так, що його вершини збігаються з кінцем ліній, намальованих на попередньому кроці.

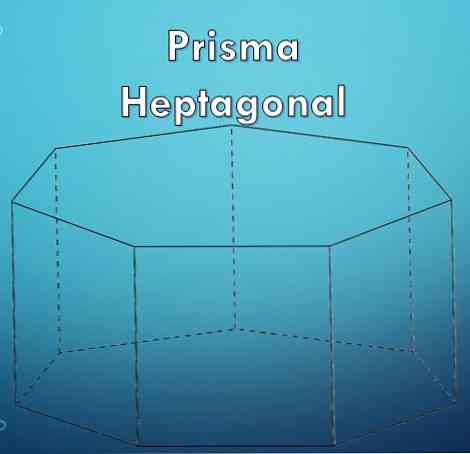
Зверху звернута семикутна призма називається прямою гексагональною призмою. Але ви також можете мати косу семикутну призму, подібну до тієї, що наведена на малюнку.

2. Властивості його підстав

Оскільки їхні бази є гептагонами, вони відповідають тому, що діагональне число D = nx (n-3) / 2, де "n" - кількість сторін багатокутника; у цьому випадку маємо, що D = 7 × 4/2 = 14.

Можна також бачити, що сума внутрішніх кутів будь-якого семикутника (регулярна або нерегулярна) дорівнює 900º. Це можна перевірити за допомогою наступного зображення.

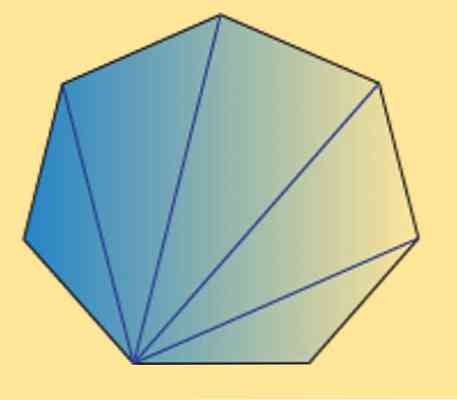
Як ви можете бачити, є 5 внутрішніх трикутників, і, використовуючи суму внутрішніх кутів трикутника, дорівнює 180º, можна отримати, що бажаний результат.

3 - Область, необхідна для побудови семикутної призми

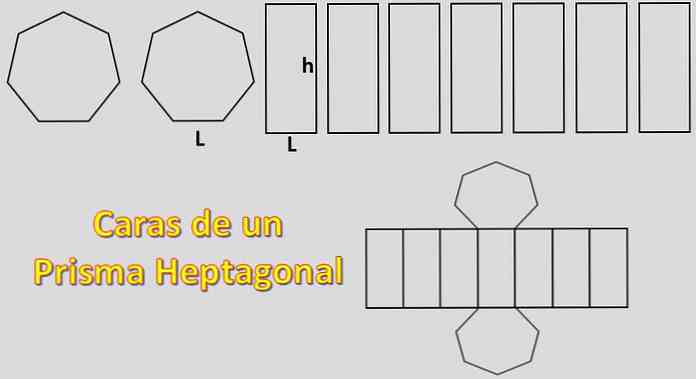
Оскільки його основи є двома семикутниками, а його сторони - сімома паралелограмами, площа, необхідна для побудови семикутної призми, дорівнює 2xH + 7xP, де "H" - площа кожного семикутника, а "P" - площа кожного паралелограма.

У цьому випадку буде обчислена площа регулярного семикутника. Для цього важливо знати визначення апотеми.

Апотема - це перпендикулярна лінія, що йде від центру регулярного багатокутника до середини будь-якої з його сторін.

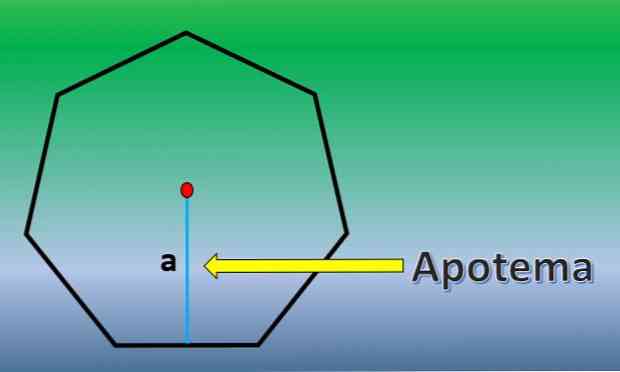
Після того, як апотема відома, площа семиугольника H = 7xLxa / 2, де "L" - довжина кожної сторони і "a" довжина апотема..

Площу паралелограма легко обчислити, визначається як P = Lxh, де "L" однакова довжина сторони семикутника і "h" - висота призми.

На закінчення, кількість матеріалу, необхідного для побудови семикутної призми (з регулярними основами), 7xLxa + 7xLxh, тобто 7xL (a + h).

4

Як тільки площа основи і висота призми відомі, обсяг визначається як (площа бази) x (висота).

У випадку семикутної призми (з регулярною базою) вона має, що її об'єм V = 7xLxaxh / 2; також може бути записаний як V = Pxaxh / 2, де "P" - периметр звичайного семикутника.

Список літератури

1. Білштейн, Р., Лібескінд, С., і Лотт, Дж. В. (2013). Математика: підхід до вирішення проблем для вчителів базової освіти. Лопес Матеос.
2. Fregoso, R. S., & Carrera, S.A. (2005). Математика 3. Редакція Progreso.
3. Gallardo, G., & Pilar, P. M. (2005). Математика 6. Редакція Progreso.
4. Gutiérrez, C.T., & Cisneros, M. P. (2005). Третій курс з математики. Редакція Progreso.
5. Kinsey, L., & Moore, T.E. (2006). Симетрія, форма і простір: вступ до математики через геометрію (проілюстровано, передрукована редакція). Springer Science & Business Media.
6. Mitchell, C. (1999). Сліпуче дизайну лінії Math (Ілюстрований ред.). Scholastic Inc.
7. Р., М. П. (2005). Я малюю 6º. Редакція Progreso.